
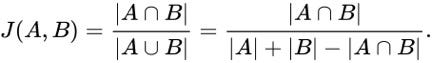
the number of common elements) over the size of the union of set A and set B (i.e. Given two sets, A and B, the Jaccard Similarity is defined as the size of the intersection of set A and set B (i.e. The Jaccard Similarity, also called the Jaccard Index or Jaccard Similarity Coefficient, is a classic measure of similarity between two sets that was introduced by Paul Jaccard in 1901. Let’s start with a quick introduction to the similarity metrics (warning math ahead). Those two algorithms fall into the category of similarity metrics and lead to the topic of this blog, which is to discuss the difference between the two algorithms and why I think one is better than the other. Of interest to this discussion is the expansion of the Jaccard Similarity metric to allow for comparisons of any pair of vertices, and the addition of the Overlap Coefficient algorithm. The RAPIDS cuGraph 0.7 release adds several new features. It should also be noted that I approach graph analysis from a social network perspective and tend to use the social science theory and terms, but I have been trying to use ‘vertex’ rather than ‘node’. If there is interest in a graph analytic primer, please leave me a comment below. I am assuming that the reader has a basic understanding of graph theory and graph analytics.
#JACCARD COEFFICIENT XLSTAT SERIES#
Due to the fact that the initial centers are randomly chosen, the same command kmeans(Eurojobs, centers = 2) may give different results every time it is run, and thus slight differences in the quality of the partitions.There are a wide range of graph applications and algorithms that I hope to discuss through this series of blog posts, all with a bias toward what is in RAPIDS cuGraph. This is the case because the k-means algorithm uses a random set of initial points to arrive at the final classification. Note that k-means is a non-deterministic algorithm so running it multiple times may result in different classification. Nstart for several initial centers and better stability However, it is more insightful when it is compared to the quality of other partitions (with the same number of clusters! see why at the end of this section) in order to determine the best partition among the ones considered. This value has no real interpretation in absolute terms except that a higher quality means a higher explained percentage. (BSS <- model$betweenss) # 4823.535 (TSS <- model$totss) # 9299.59 # We calculate the quality of the partition Here is how you can check the quality of the partition in R: # BSS and TSS are extracted from the model and stored The higher the percentage, the better the score (and thus the quality) because it means that BSS is large and/or WSS is small. Where BSS and TSS stand for Between Sum of Squares and Total Sum of Squares, respectively. X <- rbind(a, b, c) # a, b and c are combined per rowĬolnames(X) <- c("x", "y") # rename columnsīy the Pythagorean theorem, we will remember that the distance between 2 points \((x_a, y_a)\) and \((x_b, y_b)\) in \(\mathbb \times 100\% The points are as follows: # We create the points in R
#JACCARD COEFFICIENT XLSTAT HOW TO#
Therefore, before diving into the presentation of the two classification methods, a reminder exercise on how to compute distances between points is presented. Note that for hierarchical clustering, only the ascending classification is presented in this article.Ĭlustering algorithms use the distance in order to separate observations into different groups. See more clustering methods in this article.īoth methods are illustrated below through applications by hand and in R. For this reason, k-means is considered as a supervised technique, while hierarchical clustering is considered as an unsupervised technique because the estimation of the number of clusters is part of the algorithm. The first is generally used when the number of classes is fixed in advance, while the second is generally used for an unknown number of classes and helps to determine this optimal number. The two most common types of classification are:

An illustration of intercluster and intracluster distance.


 0 kommentar(er)
0 kommentar(er)
